การออกแบบแผ่นเหล็กรองใต้เสาที่รับโมเมนต์และแรงอัดตามแนวแกน (Design of steel column base plate for eccentricities)
การออกแบบแผ่นเหล็กรองใต้เสาที่รับทั้งโมเมนต์และแรงอัดในเวลาเดียวกันนั้น เราจะใช้การวิเคราะห์ที่เรียกว่าการวิเคราะห์แบบอิลาสติกครับ โดยที่สมมติว่าหน่วยแรงกดที่เกิดขึ้นใต้แผ่นเหล็กกระจายแผ่เป็นแบบเชิงเส้นซึ่งสามารถหาได้จากการรวมผลที่เกิดจากแรงอัดและโมเมนต์เข้าด้วยกัน
.
การออกแบบความกว้างและความยาวของแผ่นเหล็กเราจะใช้วิธี Trial & Error ครับ เพื่อเช็คว่าหน่วยแรงกด (bearing stress) ของฐานรองรับ เช่น ตอม่อคอนกรีต มีค่าไม่เกินกว่ามาตรฐานที่กำหนดไว้ ส่วนความหนาของแผ่นเหล็กก็จะพิจารณาจากโมเมนต์ดัดตรงหน้าตัดวิกฤต (0.8bf) ซึ่งส่วนที่เลยออกมาจากช่วงหน้าตัดวิกฤตจะมีพฤติกรรมเหมือนคานยื่นนะครับ (ตามรูปที่ 2)
.
ถ้าเราสมมติให้ความกว้างของแผ่นเท่ากับ B และความยาวเท่ากับ N ซึ่งจะต้องรับแรงอัด P และโมเมนต์ M แล้ว
หน่วยแรงที่เกิดขึ้นจะมีค่าเท่ากับ >>> fpmax = P/BN + 6M/BN^2 และ fpmin = P/BN – 6M/BN^2
ซึ่งค่า fpmax ที่ได้จะต้องมีค่าน้อยกว่า Fp ของฐานคอนกรีตที่ได้กำหนดไว้ (Fp = 0.35fc’ : เมื่อแผ่นเหล็กคลุมเต็มเนื้อคอนกรีต และ Fp = 0.35fc(sqrtA2/A1) : เมื่อแผ่นเหล็กคลุมไม่เต็มเนื้อคอนกรีต)
การที่แผ่นเหล็กรองใต้เสารับแรงตามแนวแกน P และโมเมนต์ดัด M แล้ว แผ่นเหล็กรองใต้เสาจะมีพฤติกรรมการรับแรงเยื้องศูนย์ P ซึ่งกระทำห่างจากจุดศูนย์กลางที่ระยะ e ครับ (ซึ่งค่า e ก็คือระยะเยื้องศูนย์ซึ่งมีค่าเท่ากับอัตราส่วนระหว่างโมเมนต์ดัด M และแรงตามแนวแกน P ; e = M/P)
.
ดังนั้นเราจะแบ่งการรับแรงเยื้องศูนย์เป็น 3 กรณีนะครับคือ
1. เมื่อโมเมนต์ดัดมีค่าน้อย e <= N/6
ในกรณีนี้ แรงกดใต้แผ่นเหล็กจะกระจายเป็นรูปสี่เหลี่ยมคางหมู (รูปที่ 3A)
ซึ่งค่าหน่วยแรงกดที่ขอบด้านรับแรงอัดจะเท่ากับ fpmax = P/BN(1 + 6e/N)
แต่ถ้า e มีค่าเท่ากับ N/6 ค่า fpmax จะเท่ากับ 2P/BN และหน่วยแรง fpmin = 0
.
2. เมื่อโมเมนต์ดัดมีค่าปานกลาง N/6 < e <= N/2
กรณีนี้ถ้า e < N/2 จะมีหน่วยแรงกดใต้แผ่นเหล็กแค่บางส่วนเท่านั้นครับ และกระจายเป็นรูปสามเหลี่ยม (รูปที่ 3B)
หน่วยแรงที่ขอบด้านรับแรงอัดมีค่าเท่ากับ fpmax <= Fpmax และระยะ A มีค่าเท่ากับ fpmin = 0 (จะไม่นำแรงดึงใน anchor bolt มาพิจารณา เพราะสมมติว่าแรงลัพธ์ที่ได้จากหน่วยแรงกด C กระทำที่ระยะ e ห่างจากศูนย์กลางเสา)
จากสมดุลแรง Sum(Fy) = 0 ; P = C = ½(ABfpmax) โดยที่ระยะ A gmjkdy[ 3(N/2 – e)
หน่วยแรงกดสูงสุดจะมีค่าเท่ากับ fpmax = 2P/AB
.
3. โมเมนต์ดัดมีค่ามาก e > N/2
กรณีนี้หน่วยแรงกดใต้แผ่นเหล็กจะเหมือนในกรณีที่ 2 แต่แรงลัพธ์จากหน่วยแรงกด C จะมีค่าน้อยกว่าแรงอัด P (ตามรูปที่ 3C) ดังนั้นในกรณีนี้ต้องใช้ anchor bolt เพื่อรับแรงดึงด้วย
ถ้าให้ fpmax เป็รหน่วยแรงกดสูงสุดที่เกิดขึ้น จะพิจารณาหาค่าของระยะ A และแรงดึง T ได้จากสมดุลของแรงเหมือนเดิมนะครับ
Sum(Fy) = 0 ; T + P = C = ½(ABfpmax)
จาก Sum(M) ที่แนวแรงดึง T = 0 >>> ½(fpmax*AB)(N’ – A/3) = P[e + N’ – (N/2)]
ซึ่ง N’ คือระยะจากขอบด้านรับแรงอัดถึงศูนย์กลางของ anchor bolt นะครับ
** ระยะ A ที่ต้องการจะหาได้จากสมการ T = 0
**เมื่อนำ A ไปแทนค่าใน T + P = C แล้ว จะได้ค่าแรงดึง T ที่ bolt จะต้องรับครับ
.
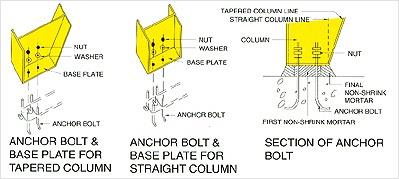
เรื่องนี้อาจจะไม่ค่อยได้พูดถึงนะครับ แต่เป็นเรื่องที่สำคัญมากเหมือนกัน เพราะโครงสร้าง PEB ที่เป็นเฟรม ถึงแม้ว่าบางคนจะโมเดลให้ฐานเป็น Pin แต่ถ้าเสาไม่ได้อยู่ที่ตำแหน่งกึ่งกลางของแผ่น plate ยังไง plate ก็ต้องรับโมเมนต์อยู่ดี จึงอยากจะพูดคุยถึงเรื่องนี้กันซักหน่อยครับ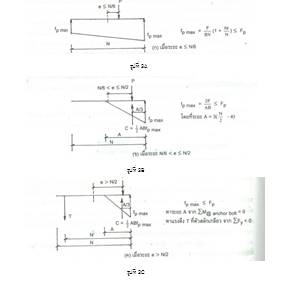

แหล่งที่มา : AirPEB-iFactory
